Faszinierend Winkel Zwischen Zwei Vektoren Berechnen Bilder. Eine häufig gefragte anwendung des skalarprodukts im abitur ist die berechnung räumlicher winkel, z.b. Gib hier die vektoren ein, deren schnittwinkel du berechnen willst.
Alle vektoren, die der gleichen relativen verschiebung entsprechen, kann man zu einer vektorklasse zusammenfassen.
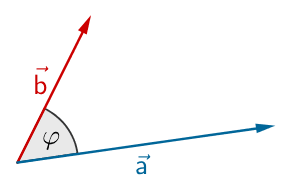
Das skalarprodukt dient zur berechnung des winkels, den zwei vektoren miteinander einschließen. Einheitvektoren, die winkel zwischen den paaren von vektoren, die winkelhalbierenden vektoren und die richtungswinkel des vektors a. Für den winkel zwischen zwei vektoren gilt nämlich aufgrund von gleichung (11): Dann bist du hier genau richtig.